Core Concepts
In this tutorial on quantum numbers, you will learn how we can describe the properties of an electron in an associated atom. These various properties include energy level, shape, orientation, and spin. You will also learn about orbital shapes.
Topics Covered in Other Articles
- Electron Configuration
- Orbitals & Orbital Shapes
Vocabulary
Nodes = a point or plane of zero electron density
Introduction to Quantum Numbers & Orbital Shapes
Quantum numbers are used to describe atomic orbitals, regions of space in which an electron can be found. From these numbers, we can determine the different properties of electrons in an atomic orbital. It is important to note that each electron will be unique to another, according to the Pauli Exclusion Principle. For this to be true, no two electrons in the same atom can have the same four quantum numbers.
The Principal Quantum Number (n)
The principal quantum number (![]() ) describes the electron shell, or the size, of an orbital. An electron shell can be thought of as the part of an atom where an electron orbits the nucleus. Learn about how Rutherford discovered the nucleus.
) describes the electron shell, or the size, of an orbital. An electron shell can be thought of as the part of an atom where an electron orbits the nucleus. Learn about how Rutherford discovered the nucleus.
The only allowable values of n are whole number integers starting from 1. A higher ![]() value means that the associated electron is farther away from the nucleus. For example, an electron with
value means that the associated electron is farther away from the nucleus. For example, an electron with ![]() would be much closer to the nucleus than an electron with
would be much closer to the nucleus than an electron with ![]() . When comparing electrons with the same
. When comparing electrons with the same ![]() , we can also say that an electron with a higher
, we can also say that an electron with a higher ![]() value is higher energy. With higher
value is higher energy. With higher ![]() , an electron will not feel the attractive pull of the positively-charged nucleus due to its farther distance. The electron’s negative charge is not stabilized, so the electron is higher energy.
, an electron will not feel the attractive pull of the positively-charged nucleus due to its farther distance. The electron’s negative charge is not stabilized, so the electron is higher energy.
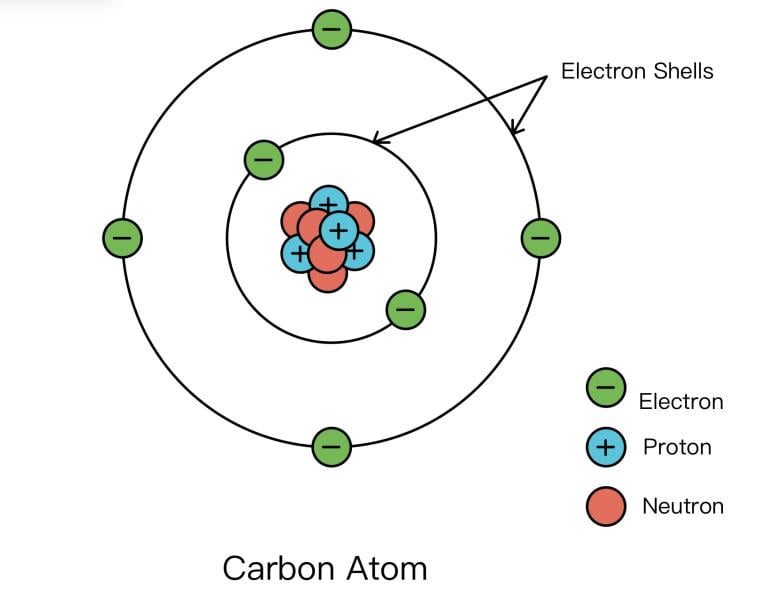
 and the outer circle being
and the outer circle being  . As we increase in
. As we increase in  , we move farther away from the nucleus.
, we move farther away from the nucleus.Orbital Shapes – The Angular Momentum Quantum Number (l)
There are four different kinds of orbitals, which are named s, p, d and f orbitals. They each have a different orbital shape. An s-orbital is spherical with the nucleus at its center. A p-orbital is dumbbell-shaped and four out of five d-orbitals are cloverleaf shaped. The last d-orbital is an elongated dumbbell with a donut around its center.
The angular momentum quantum number (![]() ) describes the subshell, or the shape, of an orbital, and its allowable range is (
) describes the subshell, or the shape, of an orbital, and its allowable range is (![]() ). There are four distinct shapes to remember: the s, p, d, and f orbitals. The value of
). There are four distinct shapes to remember: the s, p, d, and f orbitals. The value of ![]() assigned to each subshell is based on the number of angular nodes (planes). For s orbitals, which are spheres, there is no angular node, so
assigned to each subshell is based on the number of angular nodes (planes). For s orbitals, which are spheres, there is no angular node, so ![]() . For p orbitals, which has electron density separated by one angular node,
. For p orbitals, which has electron density separated by one angular node, ![]() . Following this trend, d orbitals would have
. Following this trend, d orbitals would have ![]() and f orbitals would have
and f orbitals would have ![]() , as they have two and three angular nodes, respectively.
, as they have two and three angular nodes, respectively.

 . The p orbital’s lobes are separated by a nodal plane oriented along the x axis, making
. The p orbital’s lobes are separated by a nodal plane oriented along the x axis, making  . The d orbital has two nodal planes along the x and y axis, which assigns
. The d orbital has two nodal planes along the x and y axis, which assigns  . Try drawing a f orbital and make sure to include the three angular nodes (
. Try drawing a f orbital and make sure to include the three angular nodes ( )!
)!The Magnetic Quantum Number (ml)
The magnetic quantum number (![]() ) describes the various orientations of subshells in 3D space. Its range is (
) describes the various orientations of subshells in 3D space. Its range is (![]() ), meaning that for how many ways you can uniquely rotate a certain shape, you have that many possible
), meaning that for how many ways you can uniquely rotate a certain shape, you have that many possible ![]() values. Because there is not a new, distinct orientation when you rotate a sphere around the origin, the s orbital will only have one possible magnetic orientation. But due to the angular nodes of the p, d, and f orbitals, they have many possible
values. Because there is not a new, distinct orientation when you rotate a sphere around the origin, the s orbital will only have one possible magnetic orientation. But due to the angular nodes of the p, d, and f orbitals, they have many possible ![]() values, as indicated in the diagram below.
values, as indicated in the diagram below.

The Spin Quantum Number (ms)
The spin quantum number (![]() ) describes the spin of a certain electron in an orbital. The spin is either +/- ½, which denotes either an up spin or a down spin. Each orbital can hold a max of two electrons, and if fully filled, the electrons cannot share the same spin direction. If electrons do not point in the opposite direction, then it would be a violation of the Pauli Exclusion Principle — two electrons cannot share the same four quantum numbers. If the orbital is not fully occupied, then the electron can take on any spin direction. Convention usually assigns the up spin first in a non-fully occupied orbital.
) describes the spin of a certain electron in an orbital. The spin is either +/- ½, which denotes either an up spin or a down spin. Each orbital can hold a max of two electrons, and if fully filled, the electrons cannot share the same spin direction. If electrons do not point in the opposite direction, then it would be a violation of the Pauli Exclusion Principle — two electrons cannot share the same four quantum numbers. If the orbital is not fully occupied, then the electron can take on any spin direction. Convention usually assigns the up spin first in a non-fully occupied orbital.
Orbital Shapes Practice Problems
Problem 1
What is the principal quantum number (![]() ) and the angular momentum quantum number (
) and the angular momentum quantum number (![]() ) that describes the three unpaired valence electrons of nitrogen?
) that describes the three unpaired valence electrons of nitrogen?
Problem 2
How many ![]() values do the electrons of copper (Cu) have?
values do the electrons of copper (Cu) have?
Orbital Shapes Practice Problem Solutions
1: ![]()
2: 5 (![]() )
)

